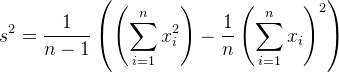
Mittlerweile hat die statistische Analyse der Raw-Daten meiner Canon 5D Mark II noch einiges an Zusatzergebnissen geliefert, die ich nach und nach in einer kleinen Serie “Raw-Analyse” posten werde. Teile des vorherigen Posts müssen dabei (leicht) korrigiert werden.
Erstes Thema ist die Varianz als wichtigste Kenngröße der Raw-Analyse, denn damit lassen sich aus der Signalstatistik etliche wichtige Kenngrößen der Kamera ableiten.
Die Varianz ist die mittlere quadratische Abweichung der Meßwerte vom Mittelwert, mit kleinen Tücken bei der Berechnung. Für die Zwecke der Raw-Analyse ist wichtig, dass bei der Addition mehrerer stochastisch unabhängiger Zufallswerte die Gesamtvarianz gleich der Summe der Einzelvarianzen ist. Das, was typischerweise als Rauschen bezeichnet wird, hat als Amplitude die Standardabweichung, also die Quadratwurzel aus der Varianz.
Um das nun mit Raw-Dateien zu machen, wird direkter Zugriff auf die echten “Roh”daten benötigt, Raw-Konverter wie Lightroom machen auch bei “alles auf Null” viele nichtlineare Umrechnungen. Aber netterweise gibt es das Tool dcraw, das im -D “Document mode” tatsächlich die echten ADU-Werte liefert. Bei der 5D Mark II mit einem 14 bit AD-Konverter sind das Werte zwischen 0 und 16383.
Naiver Ansatz wäre nun, einfach Mittelwert und Varianz der gesamten Rohdaten einer Datei zu berechnen. Das funktioniert so leider nicht. Zum einen müssen bei Flats die Farbkanäle getrennt betrachtet werden, da die einzelnen RGGB-Pixel unterschiedlich belichtet werden. Zum anderen variieren die Rohdaten auch deterministisch (lokal unterschiedliche Empflindlichkeit der Pixel und Verstärker, Abschattungen bei Flats).
Ein Versuch der Abhilfe ist nur einen kleinen Bildausschnitt in der Sensormitte zu verwenden, um zumindest bei den Flats Belichtungsunterschieden aus dem Weg zu gehen. Bei Darks ist aber auch das nur die halbe Miete. Um tatsächlich die stochastische Varianz, also das eigentlich Rauschen, zu erfassen, bietet sich das von Craig Stark und T. M. C. Abbott beschriebene Verfahren an: die Varianz aus der Differenz zwei Rohdatensätze unter ansonsten gleichen Bedingungen (Belichtung, Temperatur) zu berechnen.
Mittelwert = ( Mittelwert(Daten1) + Mittelwert(Daten2) ) / 2
Varianz = Varianz(Daten1 – Daten2) / 2
Die Varianz der Differenz ergibt sich als Summe der Einzelvarianzen (Subtraktion von Zufallsgrößen verhält sich hier wie Addition), daher der Faktor 1/2.
Bei einer Anzahl von Raw-Dateien unter gleichen Bedingungen kann das jeweils paarweise erfolgen und in der Gesamtheit zur Reduzierung der Streuung zusätzlich gemittelt werden.
Zu Automatisierung dieser Berechnung hab ich kleines Perl-Skript entwickelt, verfügbar hier auf github.
Im direkten Vergleich der Methoden zeigen sich insbesondere bei Darks deutliche Unterschiede. Hier zwei Darks bei ISO 800, 360 s Belichtungszeit, einer Umgebungstemperatur von 7 °C und 100 x 100 Pixel in der Bildmitte.
Varianz der Darks-Einzeldateien: 159,2 und 158,8
Varianz der Darks-Differenz: 116,6
Bei Bias ist der Unterschied dagegen fast zu vernachlässigen.
Varianz der Bias-Einzeldateien: 63,6 und 62,9
Varianz der Bias-Differenz: 60,5
Alle Betrachtungen in der weiteren Raw-Analyse werden im Interesse der Konsistenz immer mit Differenz-Varianz gemacht und nur unter Verwendung der G-Pixel.